Unveiling the Enigma: What Are the 3 Undefined Terms of Geometry?
In the realm of mathematics, where logic reigns supreme and order is paramount, there exist fundamental truths upon which entire systems are built. Geometry, the study of shapes, sizes, and spatial relationships, is no exception. But what if we were to tell you that at the very heart of this precise and structured world lie three enigmatic concepts, forever undefined?
Imagine embarking on a journey into a world where the building blocks themselves are shrouded in mystery. This is the world of the three undefined terms of geometry, concepts so fundamental that they defy precise definition yet form the bedrock upon which all geometric knowledge rests.
These terms, like ancient secrets whispered through generations, have intrigued mathematicians for centuries. Their very nature sparks curiosity and invites us to contemplate the limits of definition and the elegance of abstraction in mathematics.
Why are these terms left undefined, you might ask? Is it a matter of mathematical convenience, or is there a deeper philosophical reason lurking beneath the surface? The answer, like the terms themselves, is both intriguing and elusive.
Join us as we delve into the fascinating world of points, lines, and planes - the three undefined terms that hold the key to unlocking the secrets of geometry. Prepare to have your preconceptions challenged and your understanding of the mathematical world forever changed.
These three terms - point, line, and plane - may seem simple at first glance, but their lack of formal definition is deliberate and essential. By leaving them undefined, mathematicians are able to build upon a foundation of shared understanding, allowing these concepts to adapt and remain consistent across different branches and applications of geometry.
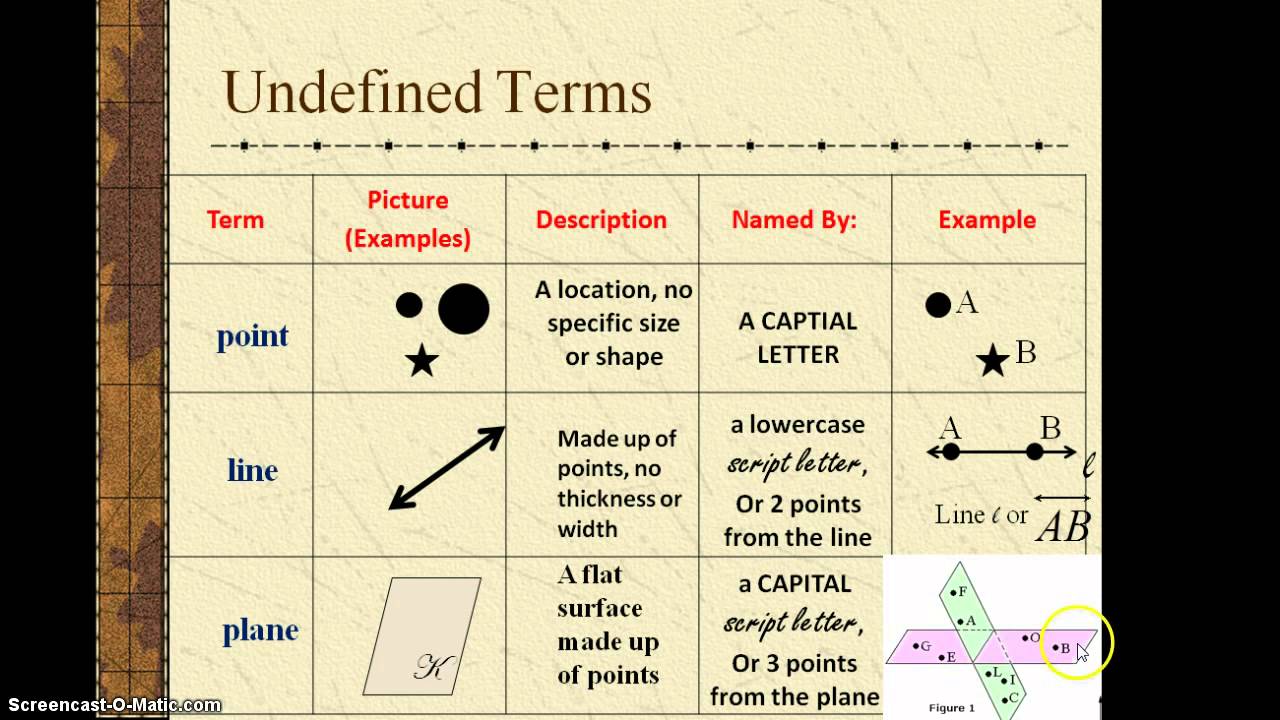
Think of a point. What is it, exactly? You might envision a tiny dot on a page, but is it truly a point, or merely a representation of one? A point, in the abstract realm of geometry, has no size, shape, or dimension. It is simply a location, a singularity in space.
Now, envision a line. Is it a straight mark drawn with a ruler? Not quite. In geometry, a line extends infinitely in both directions, possessing no thickness or curvature. It is defined solely by the points it contains and the relationship between them.
Finally, picture a plane. Not the kind that soars through the air, but a flat surface that stretches infinitely in all directions. Like a line, it has no thickness, existing solely as a two-dimensional expanse defined by the points and lines it contains.
These three undefined terms are not merely academic curiosities; they form the bedrock upon which all geometric axioms, postulates, and theorems are built. From the simplest triangle to the most complex hyperbolic geometry, all geometric concepts can be ultimately traced back to these fundamental building blocks.
Understanding the undefined nature of point, line, and plane allows us to grasp the elegance and power of abstraction in mathematics. These terms are not limited by physical constraints or concrete definitions. They can be adapted and applied to various contexts, forming the language with which we describe and explore the geometric universe.
As you delve deeper into the world of geometry, remember the undefined terms that form its foundation. They serve as a constant reminder that even in the most precise of sciences, there is always room for wonder, mystery, and the power of the undefined.
Unlock learning free printable worksheets kindergarten
Semakan bantuan zakat sabah your guide to checking zakat assistance
Placar de jogos de hoje your portal to the thrill of live scores