Unlocking Trigonometry: Your Guide to Mastering Triangles and Beyond
Have you ever looked up at a star-studded sky and wondered about the vastness of space, or marveled at the intricate architecture of a bridge? These wonders, and countless others, are underpinned by the principles of trigonometry. Trigonometry, at its core, is the study of relationships between angles and sides in triangles. It's a branch of mathematics that extends far beyond the classroom, finding applications in fields like architecture, engineering, astronomy, and even music.
Now, imagine having a treasure trove of trigonometry knowledge at your fingertips – a collection of meticulously crafted questions paired with clear, concise answers. This is the power of a trigonometry questions and answers PDF. Whether you're a student grappling with the unit circle or a professional brushing up on forgotten concepts, these PDFs offer a structured and accessible path to mastering trigonometry.
The roots of trigonometry can be traced back to ancient civilizations, with contributions from Babylonian astronomers, Egyptian surveyors, and Greek mathematicians like Hipparchus and Ptolemy. Initially developed for astronomy and navigation, its use expanded as mathematicians uncovered its versatile applications in various fields. The development of the unit circle and trigonometric identities further enriched the subject, making it an indispensable tool for solving complex problems involving angles, distances, and periodic phenomena.
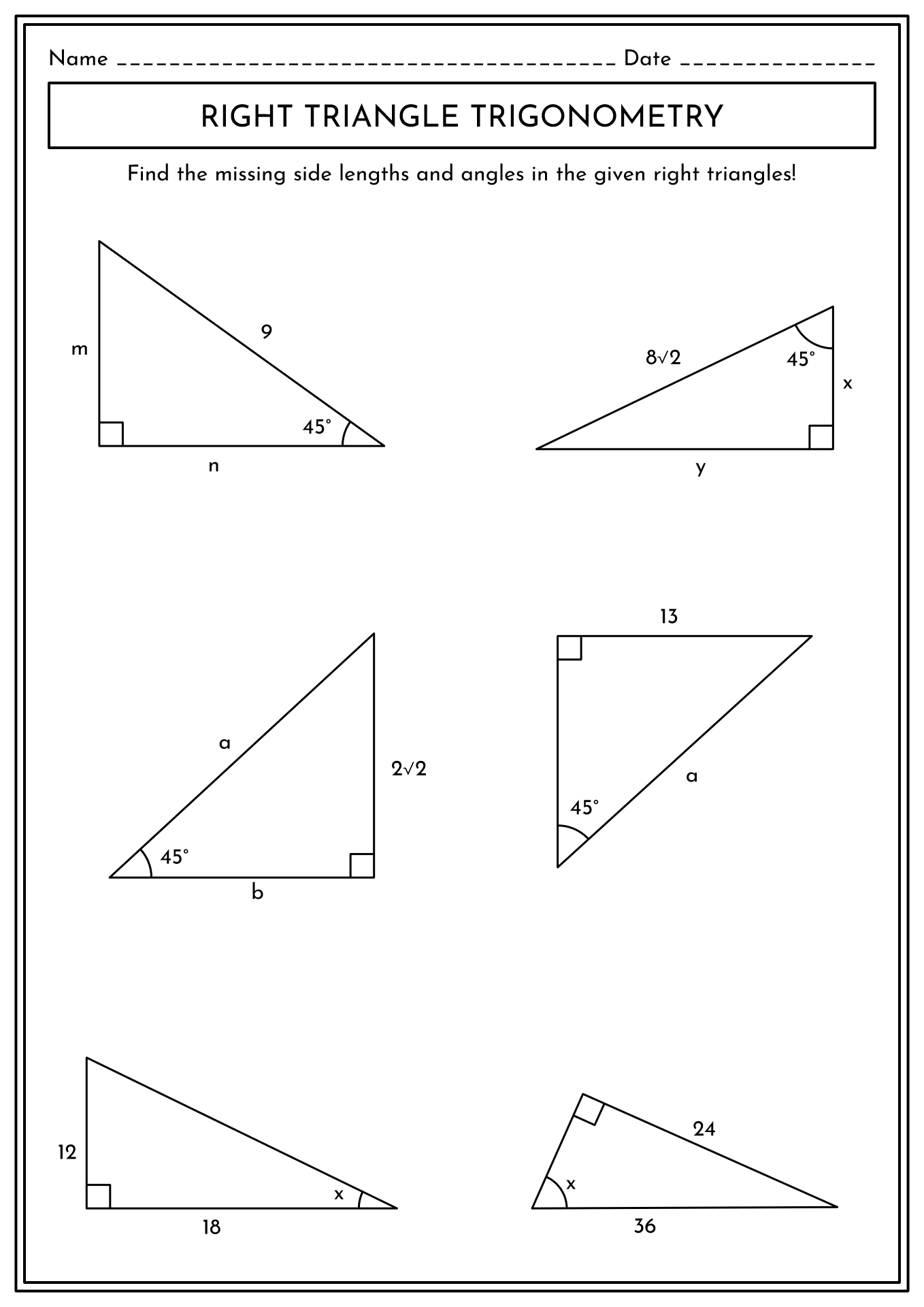
One of the central issues in trigonometry is understanding the relationship between the angles and sides of a right triangle. This is where the trigonometric ratios – sine, cosine, and tangent – come into play. These ratios, often abbreviated as sin, cos, and tan, provide a way to relate the lengths of the sides to the angles within the right triangle. Mastering these ratios forms the foundation for solving a wide array of trigonometric problems.
Let's consider a simple example. Imagine a right triangle where one angle is 30 degrees, and the hypotenuse (the side opposite the right angle) is 10 units long. Using the sine ratio, defined as the opposite side divided by the hypotenuse (sin θ = opposite/hypotenuse), we can calculate the length of the side opposite the 30-degree angle. In this case, sin 30° = 1/2, so the opposite side would be (1/2) * 10 = 5 units long.
Advantages and Disadvantages of Trigonometry Questions with Answers PDFs
| Advantages | Disadvantages |
|---|---|
| Accessible and convenient for self-study | May not cover all topics comprehensively |
| Provide a structured approach to learning | Can become repetitive if used exclusively |
| Offer immediate feedback on problem-solving skills | Limited opportunity for asking clarifying questions |
While trigonometry can be challenging, its mastery opens doors to understanding our world in profound ways. From the graceful curves of a suspension bridge to the intricate dance of sound waves, trigonometry provides the tools to analyze, predict, and create. So, embrace the challenge of learning trigonometry – your journey begins with a single angle.
Unlocking opportunities the benefits of using credit cards wisely
Crafting your tranquil tech oasis a guide to iphone home screen aesthetics
Unlocking the power of pngs instagram facebook visuals