Mastering Center of Gravity Calculations
Ever wonder how acrobats balance effortlessly or why some objects tip over so easily? The secret lies in understanding the center of gravity. This seemingly complex concept is actually quite approachable, and knowing how to determine the center of gravity is a valuable skill applicable in various fields.
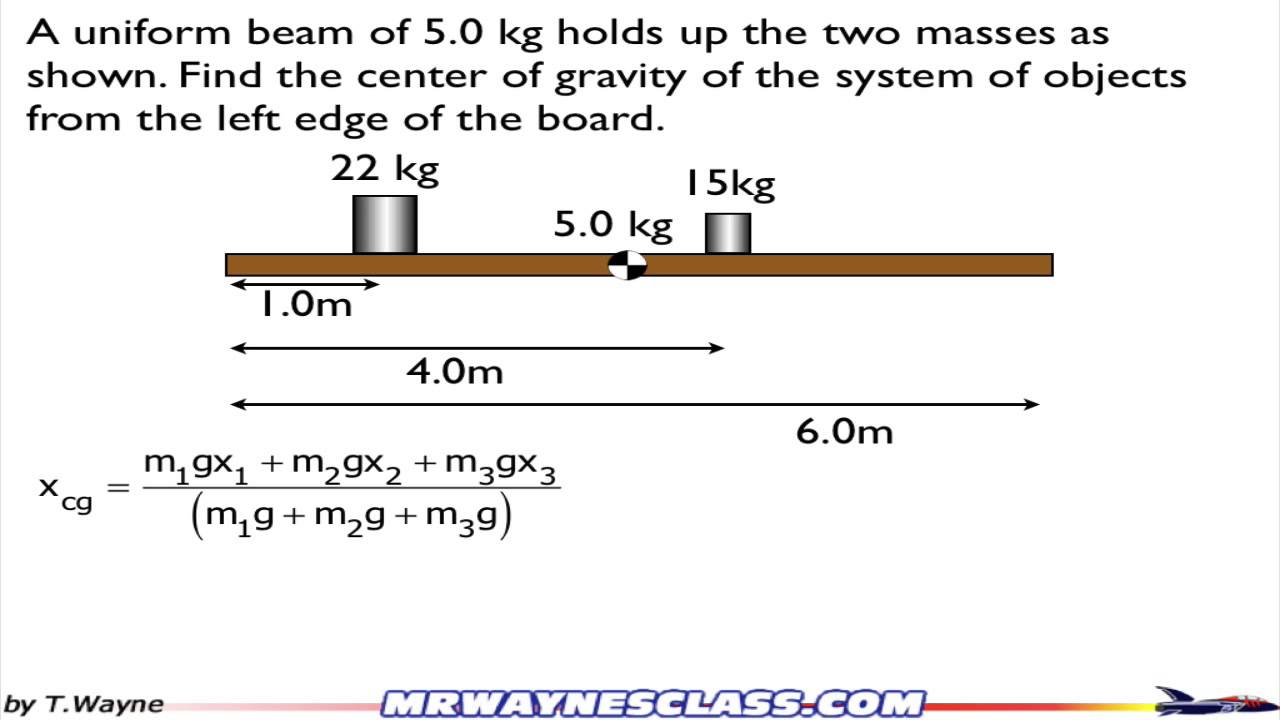
Determining the center of gravity, sometimes referred to as the center of mass, is essentially finding the average location of an object's weight. Imagine an object as a collection of tiny particles, each with its own weight. The center of gravity is the point where all these individual weights balance each other out.
The concept of the center of gravity has been around for centuries. Archimedes, a Greek mathematician and scientist, is credited with some of the earliest work on this topic in the 3rd century BC. He developed methods for finding the center of gravity of various shapes, laying the foundation for future understanding.
The ability to pinpoint an object's center of gravity is crucial in numerous fields. From engineering and architecture to animation and physics simulations, it plays a vital role in design and analysis. Understanding how to determine center of gravity allows engineers to build stable structures, animators to create realistic movements, and physicists to predict object behavior.
One of the primary challenges in center of gravity determination is dealing with complex shapes. While simple geometric shapes have easily defined centers of gravity, irregular objects require more sophisticated methods of calculation, often involving calculus or computational tools.
For a simple object like a uniform ruler, the center of gravity lies at its midpoint. For more complex shapes, we can often use symmetry. If an object has an axis of symmetry, its center of gravity lies on that axis. However, for irregular objects, calculating the center of gravity involves more advanced methods, often requiring summing the products of mass elements and their distances from a reference point, and then dividing by the total mass.
Benefit 1: Enhanced Stability: Knowing the center of gravity helps design stable structures by ensuring the weight is distributed evenly. For example, architects use this principle to prevent buildings from tipping over.
Benefit 2: Improved Motion Control: In robotics and animation, understanding center of gravity is essential for realistic movement. Accurately placing the center of gravity allows for more natural and predictable simulations.
Benefit 3: Optimized Design: In vehicle design, a low center of gravity enhances handling and reduces the risk of rollovers. This is why sports cars are designed with low centers of gravity.
Steps for a Simple Calculation: 1. Divide the object into smaller, regular shapes. 2. Determine the center of gravity of each shape. 3. Calculate the weighted average of these centers of gravity based on the mass or area of each shape.
Checklist for Center of Gravity Calculation: 1. Identify the shape of the object. 2. Determine if symmetry can simplify the calculation. 3. If not, divide the object into smaller shapes. 4. Calculate the weighted average of individual centers of gravity.
Advantages and Disadvantages of Center of Gravity Calculations
| Advantages | Disadvantages |
|---|---|
| Predicting stability | Complex calculations for irregular shapes |
| Optimizing designs | Requires accurate mass distribution data |
| Improving safety | Can be time-consuming for intricate objects |
Best Practice 1: Simplify complex shapes by breaking them down into simpler geometric forms. Best Practice 2: Utilize symmetry whenever possible to reduce calculations. Best Practice 3: Use appropriate software for complex or irregular shapes. Best Practice 4: Verify calculations with experimental methods if possible. Best Practice 5: Consider the distribution of mass within the object.
Example 1: Finding the center of gravity of a rectangular block. Example 2: Calculating the center of gravity of a triangular plate. Example 3: Determining the center of gravity of a semi-circular shape. Example 4: Analyzing the center of gravity of a composite object. Example 5: Calculating the center of gravity of an irregular shape using numerical methods.
FAQ 1: What is the difference between center of gravity and center of mass? FAQ 2: How do I calculate the center of gravity of a 3D object? FAQ 3: What are some common mistakes in calculating center of gravity? FAQ 4: What software can I use to calculate center of gravity? FAQ 5: Why is the center of gravity important in engineering? FAQ 6: How does the center of gravity affect stability? FAQ 7: How is center of gravity used in animation? FAQ 8: What is the role of center of gravity in vehicle design?
Tips and Tricks: For symmetrical objects, look for the axes of symmetry. The center of gravity will lie at their intersection. For irregular objects, consider using approximation methods or software tools.
In conclusion, understanding and calculating the center of gravity is a fundamental concept with wide-ranging applications. From ensuring the stability of buildings to designing efficient vehicles and creating realistic animations, mastering this skill is invaluable. While the calculations can range from simple to complex, the underlying principle remains the same: finding the point where an object’s weight is balanced. By grasping the basic concepts and utilizing the tools and techniques available, anyone can learn to effectively determine the center of gravity and leverage this knowledge in various fields. Take the time to understand these principles, and you'll unlock a deeper understanding of the world around you, from the simplest balancing act to the most complex engineering feats. Start exploring and experimenting with center of gravity calculations today and see how this knowledge can enhance your understanding and problem-solving abilities.
Free printable easter coloring pages a hunt for creative fun
Craving roast beef a deep dive into brothers roast beef quincy ma menu
Best 25 round magazine for ruger 1022 unleash your rifles potential