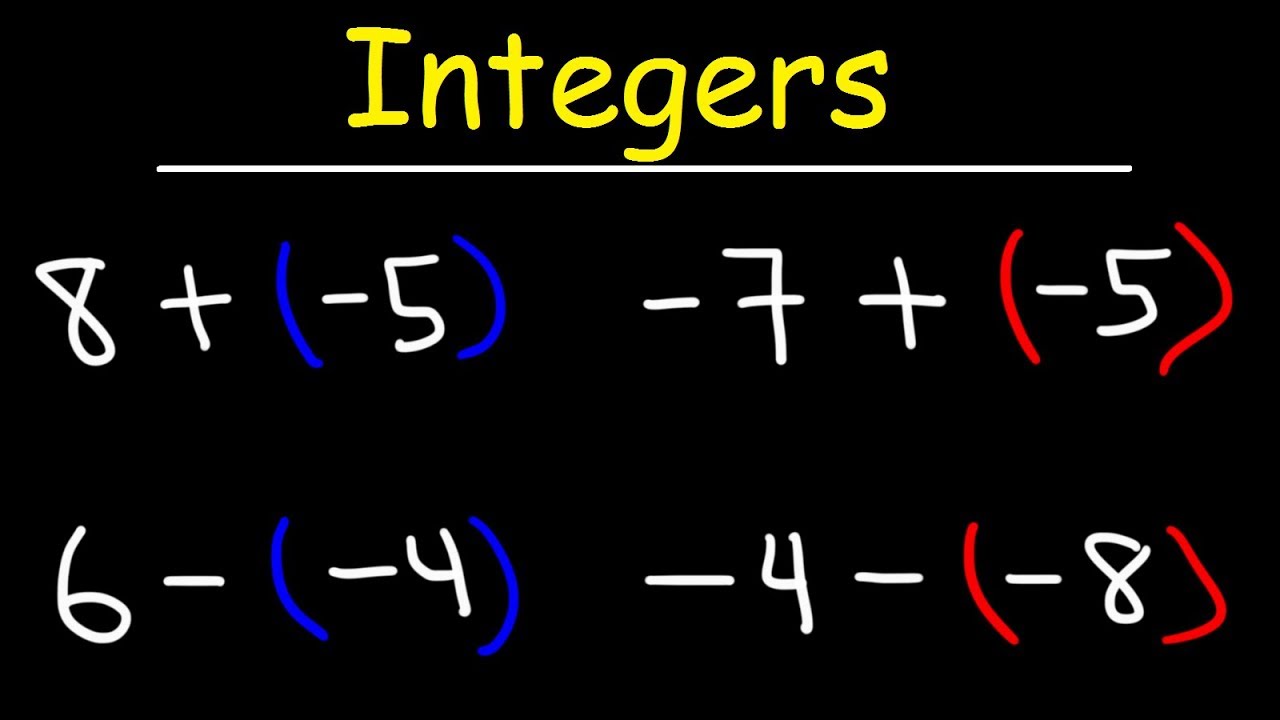Integer Arithmetic: Cracking the Code of Positive and Negative Numbers
Ever wondered how computers crunch numbers, or how scientists model complex systems? The foundation lies in understanding integers and their manipulations. This isn't just about rote memorization; it's about grasping the core principles of how numbers interact, a fundamental concept that powers everything from basic calculations to advanced algorithms. We're talking about integer arithmetic – the art of adding and subtracting positive and negative whole numbers. It's the bedrock of mathematics and a crucial skill for navigating the quantitative world.
So, what exactly does adding and subtracting integers entail? It's about expanding the familiar concept of addition and subtraction beyond positive numbers to include their negative counterparts. This seemingly simple extension opens up a world of possibilities, allowing us to represent and manipulate quantities that can increase or decrease. Think about tracking temperature changes, calculating financial gains and losses, or modeling the movement of objects in different directions. Integer arithmetic provides the tools for these and countless other applications.
The history of integer operations intertwines with the development of number systems themselves. Negative numbers weren't readily embraced. Early mathematicians grappled with the concept of quantities less than zero. However, the need to represent debts, losses, and opposite directions eventually led to the acceptance and formalization of negative numbers, paving the way for the development of integer arithmetic as we know it today. This evolution reflects the power of mathematics to adapt and expand to meet the demands of real-world problems.
The significance of integer arithmetic extends far beyond basic calculations. It forms the basis of algebra, calculus, and other advanced mathematical fields. Understanding how to manipulate integers is essential for problem-solving in science, engineering, finance, and many other disciplines. From balancing chemical equations to analyzing financial data, integer operations are the underlying language of quantitative reasoning.
One of the primary challenges in learning integer arithmetic lies in grasping the concept of negative numbers and their interaction with positive numbers. The rules for adding and subtracting integers can seem counterintuitive at first, especially when dealing with combinations of positive and negative values. However, with practice and a clear understanding of the underlying principles, these operations become second nature. Let's explore some examples: Adding 5 + (-3) is the same as 5 - 3, resulting in 2. Subtracting 5 - (-3) is equivalent to 5 + 3, yielding 8.
Performing integer calculations involves applying specific rules. When adding two positive integers, the result is the sum of their absolute values. When adding two negative integers, the result is the negative sum of their absolute values. For example: -5 + (-3) = -8.
When adding integers with different signs, subtract the smaller absolute value from the larger absolute value, and the result takes the sign of the integer with the larger absolute value. For instance, 7 + (-3) = 4.
Benefits of mastering integer arithmetic: 1. Enhanced problem-solving skills. 2. Foundation for advanced mathematics. 3. Real-world applications in various fields.
Action plan: 1. Learn the rules. 2. Practice with examples. 3. Apply to real-world scenarios.
Advantages and Disadvantages of Using Integer Arithmetic
| Advantages | Disadvantages |
|---|---|
| Precise calculations with whole numbers | Cannot represent fractional values |
| Foundation for more complex math | Potential for overflow errors in computing |
Best Practices: 1. Understand the rules of signs. 2. Use number lines for visualization. 3. Practice regularly. 4. Apply to real-life problems.
Real-world examples: 1. Calculating temperature changes. 2. Tracking financial transactions. 3. Measuring altitude differences.
Challenges: 1. Dealing with large negative numbers. Solution: Break down problems into smaller steps.
FAQs: 1. What is an integer? Answer: A whole number (positive, negative, or zero). 2. What is the difference between adding and subtracting integers? Answer: Adding combines values, while subtracting finds the difference.
Tips and Tricks: Use a number line for visualization, especially when starting out.
In conclusion, mastering integer arithmetic is not merely an academic exercise; it's a fundamental skill that empowers us to navigate the quantitative world. From basic calculations to complex problem-solving, understanding how to add and subtract integers forms the bedrock of mathematical literacy and opens doors to a wide range of applications in science, engineering, finance, and everyday life. By grasping the core principles, practicing regularly, and applying these concepts to real-world scenarios, we can unlock the full potential of integer arithmetic and enhance our ability to analyze, interpret, and interact with the world around us. Embracing the challenge of integer arithmetic ultimately equips us with a powerful tool for understanding and shaping our world. Take the time to master these concepts, and you'll find yourself equipped to tackle a wide range of mathematical challenges.
The language of legends unveiling japanese dragon tattoo color meaning
Unlocking precision the power of the fine point pilot pen
Echoes of aurora finding solace in peterson funeral home obituaries
