Gelijkzijdige Driehoek Oppervlakte Berekenen Eenvoudig Uitgelegd
Hoe bereken je de oppervlakte van een gelijkzijdige driehoek? Deze vraag komt regelmatig terug in de wiskunde en kent diverse praktische toepassingen. Of je nu een student, architect, ontwerper of gewoon nieuwsgierig bent, het begrijpen van deze berekening is waardevol.
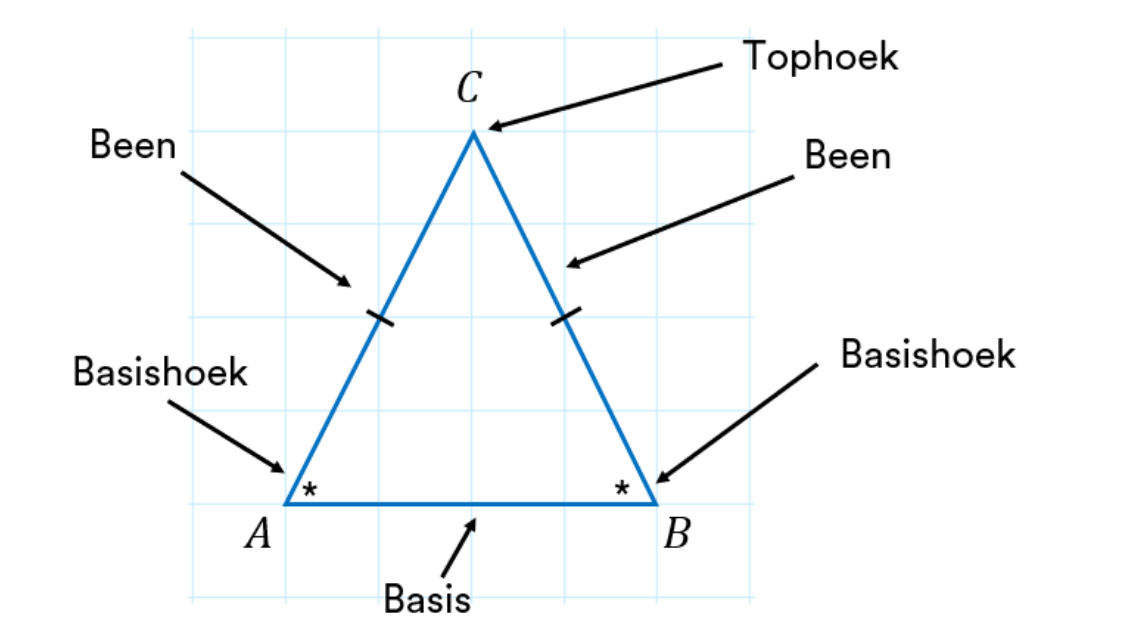
Een gelijkzijdige driehoek is een driehoek met drie gelijke zijden en drie gelijke hoeken. De oppervlakte is de ruimte binnen de driehoek. Het correct berekenen van deze oppervlakte is essentieel voor allerlei projecten, van het bepalen van de hoeveelheid materiaal die nodig is voor een driehoekig zeil tot het ontwerpen van geometrische patronen.
Het berekenen van de oppervlakte van een gelijkzijdige driehoek is relatief eenvoudig met de juiste formule. Het beheersen van deze formule opent deuren naar een beter begrip van geometrie en biedt praktische oplossingen voor alledaagse problemen.
De geschiedenis van het berekenen van de oppervlakte van een gelijkzijdige driehoek gaat terug naar de oude Grieken, met name Heron van Alexandrië. Zijn formule voor de oppervlakte van een driehoek, die ook toepasbaar is op gelijkzijdige driehoeken, is een belangrijke bijdrage aan de meetkunde.
Het belang van het kunnen berekenen van de oppervlakte van een gelijkzijdige driehoek strekt zich uit tot diverse vakgebieden. In de architectuur en bouwkunde is het cruciaal voor het ontwerpen van structuren en het berekenen van materiaalbehoeften. In de grafische vormgeving speelt het een rol bij het creëren van visueel aantrekkelijke ontwerpen. En in de natuurkunde is het relevant voor het begrijpen van krachten en evenwicht.
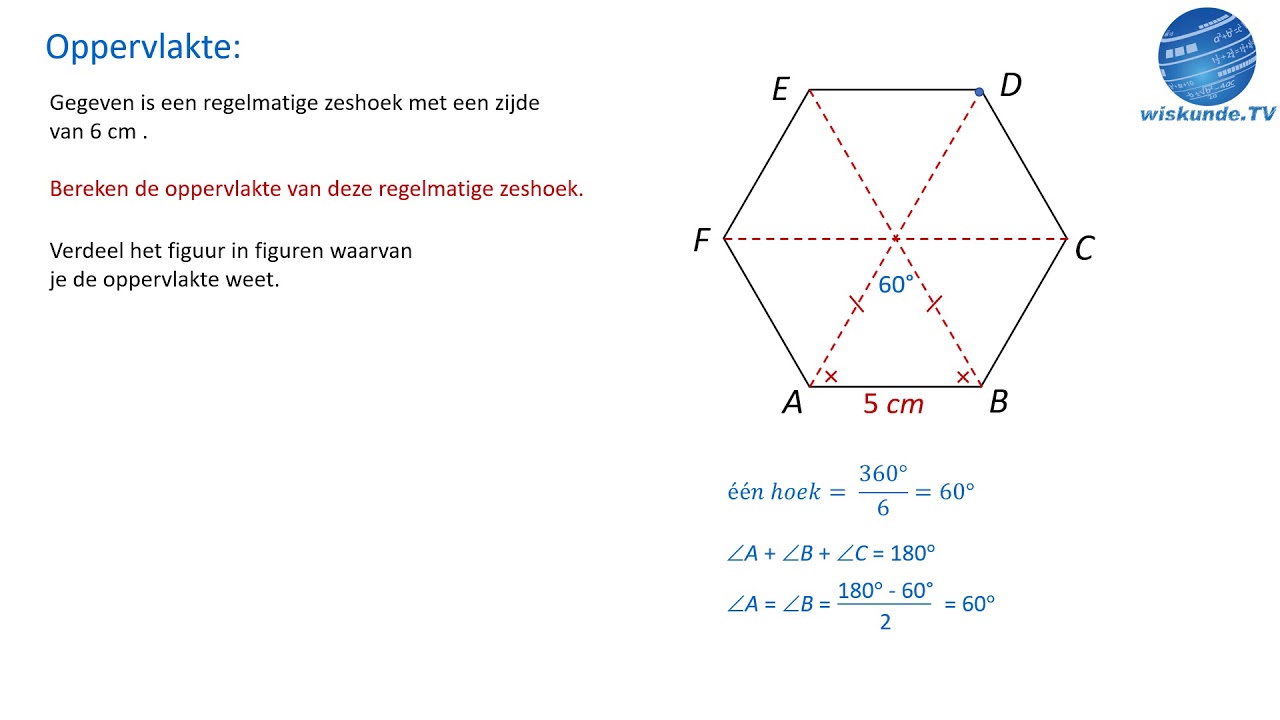
De formule voor de oppervlakte (A) van een gelijkzijdige driehoek met zijde 'z' is: A = (z²√3) / 4. Stel, een gelijkzijdige driehoek heeft een zijde van 6 cm. De oppervlakte is dan (6²√3) / 4 = (36√3) / 4 = 9√3 ≈ 15.59 cm².
Voordelen van het kennen van deze berekening zijn: 1. Nauwkeurige metingen in diverse projecten. 2. Een beter begrip van geometrische principes. 3. Vermogen om complexe problemen op te lossen.
Een actieplan om de oppervlakte te berekenen: 1. Meet de lengte van één zijde. 2. Gebruik de formule. 3. Bereken de oppervlakte.
Checklist: 1. Heb ik de zijde gemeten? 2. Heb ik de juiste formule gebruikt? 3. Is mijn antwoord realistisch?
Stap-voor-stap handleiding: 1. Meet de zijde. 2. Kwadrateer de zijde. 3. Vermenigvuldig met de wortel van 3. 4. Deel door 4.
Voor- en Nadelen Gelijkzijdige Driehoek Oppervlakte Berekenen
N.v.t.
Vijf beste praktijken: 1. Gebruik een accurate meetmethode. 2. Controleer de berekening. 3. Gebruik een rekenmachine voor complexe getallen. 4. Rond het antwoord af op een geschikt aantal decimalen. 5. Begrijp de eenheden.
Vijf voorbeelden: 1. z = 5 cm, A ≈ 10.83 cm². 2. z = 10 cm, A ≈ 43.30 cm². 3. z = 2 cm, A ≈ 1.73 cm². 4. z = 8 cm, A ≈ 27.71 cm². 5. z = 12 cm, A ≈ 62.35 cm².
Vijf uitdagingen en oplossingen: N.v.t.
FAQ: 1. Wat is een gelijkzijdige driehoek? Antwoord: Een driehoek met drie gelijke zijden. 2. Wat is de formule? Antwoord: (z²√3) / 4. 3. Wat is √3? Antwoord: Ongeveer 1.732. 4. Moet ik een rekenmachine gebruiken? Antwoord: Aanbevolen. 5. Wat zijn de eenheden? Antwoord: Vierkante eenheden (cm², m², etc.). 6. Kan ik de formule ook gebruiken voor andere driehoeken? Antwoord: Nee, alleen voor gelijkzijdige driehoeken. 7. Waar kan ik meer informatie vinden? Antwoord: Online wiskunde bronnen. 8. Wat is de praktische toepassing? Antwoord: Diverse toepassingen in wetenschap, techniek en design.
Tips: Gebruik een liniaal voor nauwkeurige metingen. Onthoud de formule.
Het berekenen van de oppervlakte van een gelijkzijdige driehoek is een fundamentele vaardigheid met brede toepasbaarheid. Of je nu een student bent die worstelt met meetkunde of een professional die nauwkeurige berekeningen nodig heeft, het beheersen van deze formule opent deuren naar een dieper begrip van wiskundige principes en praktische toepassingen. Het correct toepassen van de formule (z²√3) / 4 leidt tot accurate resultaten en stelt je in staat om diverse problemen op te lossen. Investeer tijd in het begrijpen van deze berekening en ontdek de kracht van geometrie in actie. Oefen met verschillende voorbeelden en raadpleeg online bronnen voor extra ondersteuning. De mogelijkheden zijn eindeloos wanneer je de oppervlakte van een gelijkzijdige driehoek kunt berekenen. Dus pak je rekenmachine, meet die zijde en begin met berekenen!
Waar weet ik veel van ontdek het hier
Effectief medicijnbeheer ontdek de kracht van ni medicines management nieuwsbrieven
De kosten van een volledig kunstgebit alles wat je moet weten


.png)