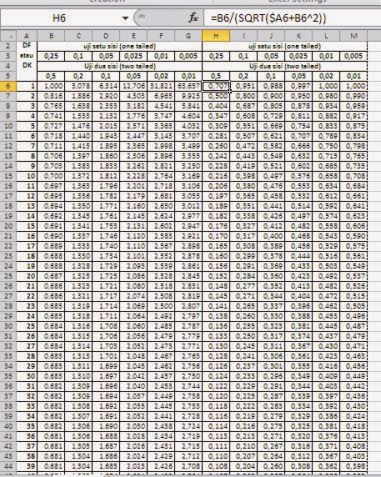
De Kracht van Correlatie: Begrijp de R Tabel Product Moment 1-100
Hoe sterk is het verband tussen twee variabelen? Deze vraag staat centraal in veel onderzoeken, en de r tabel product moment 1-100 biedt een handig hulpmiddel om die vraag te beantwoorden. Of je nu student, onderzoeker, of gewoon geïnteresseerd bent in statistiek, inzicht in deze tabel is essentieel.
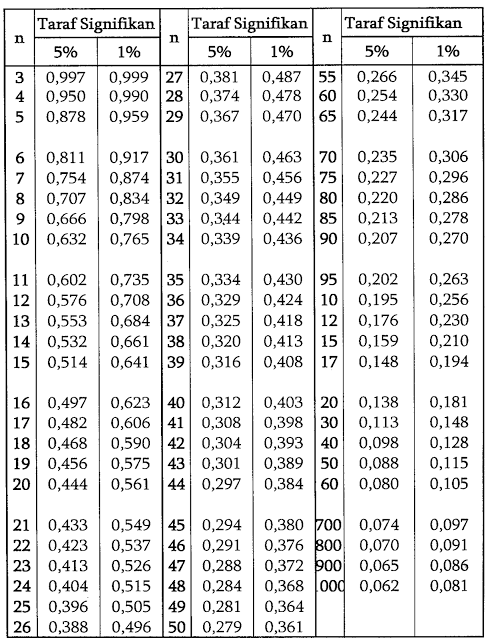
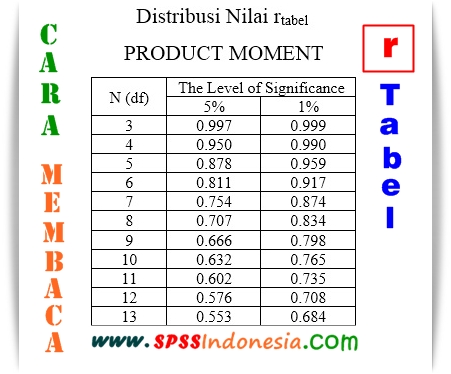
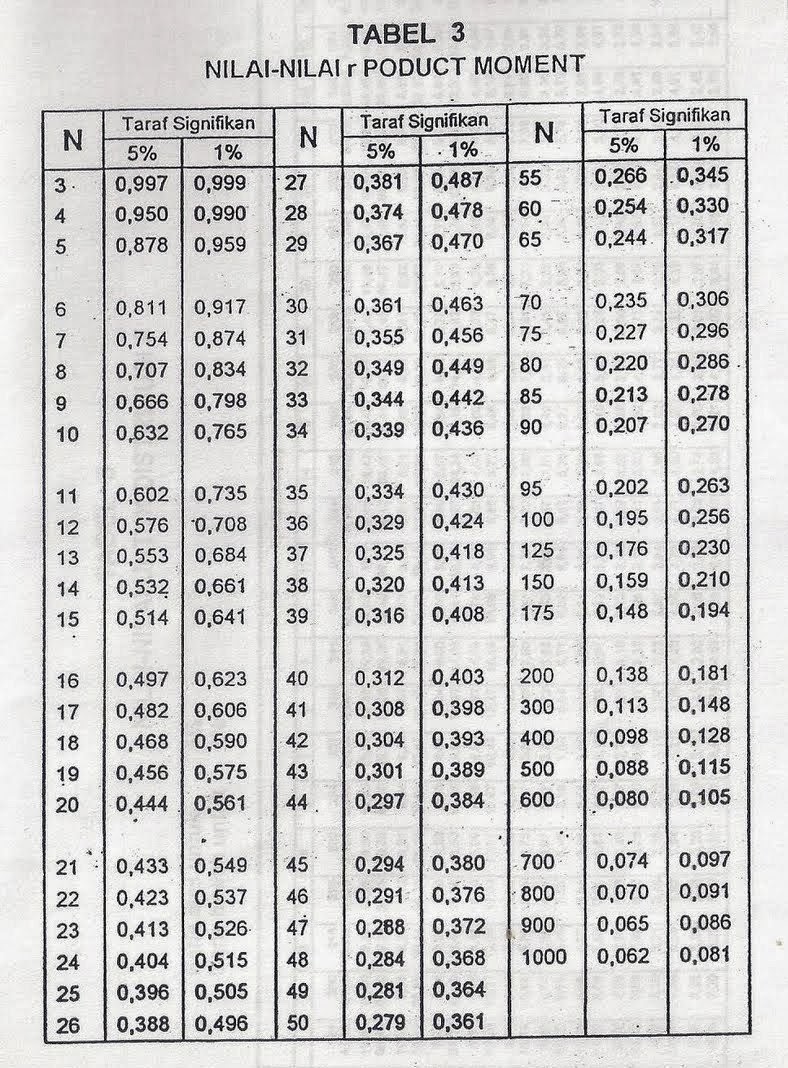
De r tabel, ook wel correlatietabel genoemd, toont de kritieke waarden voor de Pearson correlatiecoëfficiënt (r). Deze coëfficiënt meet de lineaire samenhang tussen twee variabelen op een schaal van -1 tot +1. Een waarde van -1 duidt op een perfecte negatieve correlatie, +1 op een perfecte positieve correlatie, en 0 op geen lineaire correlatie. De r tabel product moment 1-100 is specifiek ontworpen voor steekproefgroottes (n) van 1 tot 100.
Maar wat betekent dit nu precies? Stel je voor dat je de relatie tussen studietijd en cijfers wilt onderzoeken. Je verzamelt data van 50 studenten en berekent de correlatiecoëfficiënt. De r tabel product moment 1-100 helpt je vervolgens te bepalen of deze correlatie statistisch significant is, gegeven je steekproefgrootte.
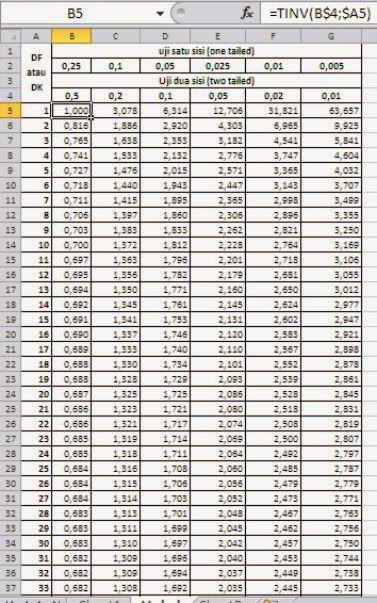
Het gebruik van de r tabel is vrij eenvoudig. Eerst bepaal je de vrijheidsgraden (df), wat gelijk is aan n-2. Vervolgens zoek je in de tabel de kritieke waarde op die overeenkomt met jouw df en het gewenste significantieniveau (alpha), meestal 0.05 of 0.01. Als de absolute waarde van jouw berekende correlatiecoëfficiënt groter is dan de kritieke waarde, is de correlatie statistisch significant.
Hoewel de exacte oorsprong van de r tabel product moment 1-100 lastig te pinpointen is, is deze onlosmakelijk verbonden met de ontwikkeling van de Pearson correlatiecoëfficiënt eind 19e eeuw. De tabel is een cruciaal instrument geworden voor het interpreteren van correlaties en speelt een belangrijke rol in diverse wetenschappelijke disciplines, van psychologie tot economie. Een veelvoorkomend probleem bij het gebruik van de tabel is het correct bepalen van de vrijheidsgraden en het kiezen van het juiste significantieniveau.
Een groot voordeel van het gebruiken van de r tabel is de eenvoud. Het biedt een snelle en efficiënte manier om de significantie van een correlatie te bepalen. Daarnaast is de tabel breed beschikbaar in statistiekboeken en online. Ten slotte zorgt het gebruik van de tabel voor een gestandaardiseerde aanpak bij het interpreteren van correlaties, wat de vergelijkbaarheid van onderzoeksresultaten bevordert.
Voor- en Nadelen R Tabel Product Moment 1-100
Het is belangrijk om te beseffen dat er ook nadelen kleven aan het gebruik van de r tabel, vooral met de komst van statistische software.
Veelgestelde Vragen:
Wat is de r tabel product moment 1-100? De r tabel toont de kritieke waarden voor de Pearson correlatiecoëfficiënt voor steekproefgroottes van 1 tot 100.
Hoe gebruik ik de r tabel? Bepaal de vrijheidsgraden (n-2) en zoek de kritieke waarde op die overeenkomt met jouw df en alpha.
Wat is een correlatiecoëfficiënt? Een maat voor de lineaire samenhang tussen twee variabelen.
Wat betekent een negatieve correlatie? Als de ene variabele stijgt, daalt de andere.
Wat betekent een positieve correlatie? Als de ene variabele stijgt, stijgt de andere ook.
Wat is statistische significantie? De waarschijnlijkheid dat een resultaat niet op toeval berust.
Waar kan ik de r tabel vinden? In statistiekboeken en online.
Wat zijn de beperkingen van de r tabel? Het is minder precies dan statistische software en beperkt tot specifieke steekproefgroottes.
Tips en trucs: Gebruik altijd de juiste vrijheidsgraden en significantieniveau. Overweeg het gebruik van statistische software voor complexere analyses.
De r tabel product moment 1-100 is een waardevol instrument voor het begrijpen van correlaties. Het biedt een eenvoudige en snelle manier om de significantie van een correlatie te bepalen. Hoewel er beperkingen zijn, blijft de tabel een belangrijk hulpmiddel voor studenten en onderzoekers. Door de principes van correlatie te begrijpen en de r tabel correct toe te passen, kunnen we waardevolle inzichten verkrijgen uit data en gefundeerde beslissingen nemen. Het is belangrijk om te onthouden dat correlatie geen causaliteit impliceert. Verder onderzoek is altijd nodig om de aard van de relatie tussen variabelen te bevestigen. Blijf leren en ontdek de fascinerende wereld van statistiek!
De betekenis van regressie in het tamil een diepgaande analyse
Non binaire namen met s een gids voor genderneutrale namen
Levensverwachting van katten met diabetes